Since a long time ago, mathematicians have shown strong interest in solving second degree equations (also known as quadratic equations), i.e. equations for which the highest degree contains x2 (by using modern usual notations). Thus, the earliest known text referring to the latter dates back to two thousand years before our era, at the time of Babylonians. It is then Al-Khwarizmi, during the 9th century, who established the formulas for the systematic solving of these equations (please refer to the links given at the end of this post for the historical aspects).
Today, the methodology for solving second degree equations is based on their canonical form. For example, if we consider the equation x2 + 2x – 3 = 0, the trinomial x2 + 2x – 3 is like the beginning of a remarkable identity. Indeed, we can write:
x2 + 2x – 3
= x2 + 2x + 1 – 1 – 3
= x2 + 2x + 1 – 4
= (x+1)2 – 4, by recognizing a remarkable identity of the first type: (a+b)2 = a2 + 2ab + b2
= (x+1)2 – 22 which is the canonical form
= (x + 1 + 2)(x + 1 – 2), by recognizing this time a remarkable identity of the third type: a2 – b2 = (a+b)(a-b)
= (x + 3)(x – 1)
And at this point, we won ![]() : by putting the factored trinomial back into our original equation, we obtain (x + 3)(x – 1) = 0.
: by putting the factored trinomial back into our original equation, we obtain (x + 3)(x – 1) = 0.
We know that a product of terms is equal to zero if and only if at least one of the terms is equal to zero (this is due to the fact that zero is the absorbing element of the multiplication operation). This rule therefore leads to the system:
or
The two solutions are thus -3 et 1 (Yippee!)
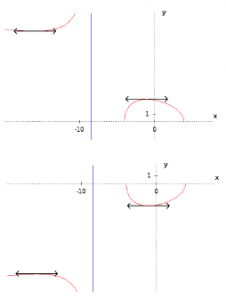
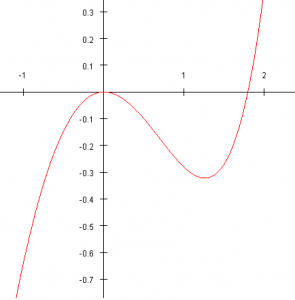
We can crosscheck our result by plotting the graph of the function f(x) = x2 + 2x – 3. We can see that the resulting curve (a parabola) intersects the x-axis at two points that seem to have x = -3 and x = 1 as first coordinate (this is obviously not a proof but more a way to verify our methodology; on the other hand, our methodology is perfectly rigorous).
By still using curves to explore solutions, we can consider the following one. We can see here that the parabola never crosses the x-axis. So, the corresponding equation should have no solutions. Indeed, the equation is here x2 + 2x + 3 = 0. By repeating the previous methodology, we obtain:
x2 + 2x + 3
= x2 + 2x + 1 – 1 + 3
= (x+1)2 + 2
It is not possible to factor further this expression as we cannot find any remarkable identity! In fact, we have here two positive terms: (x+1)2, which is a power of 2 (thus positive) and 2 which is strictly positive. The sum of these two terms is always strictly positive and therefore never reaches zero. No solution!
We have to cover one last case, where the parabola is tangent to the x-axis (cutting it at just one point). This case corresponds to the equation x2-+2x+1 = 0 whose left-hand side is directly a remarkable identity, it thus transforms itself into (x+1)2 = 0 and the solution is x = -1 (sometimes referred to as a “double root”).
We are now ready to consider the generic problem of second degree equations solving. We will start with the trinomial ax2 + bx + c, assuming a is non-zero (to ensure that we really have a second degree here). We will proceed as before, and for this we start by factoring a:
To continue, we must assume that b2 – 4ac ⩾ 0. Under this assumption, a remarkable identity of the third type appears, leading to:
We must therefore consider the case a> 0 leading to √a2 = a and the case where a <0 giving √a2 = -a. In fact, we can see that both cases lead to the same result:
The equation is then and the solutions are:
These solutions are valid under the assumption we made, i.e. b2 – 4ac ⩾ 0 . For the particular case b2 – 4ac = 0, roots can be simplified as:
and it turns out that this is one and same root, corresponding to the case where the parabola cuts the x-axis at one point.
We are close to have finalized our analysis. We still have to consider the case where b2 – 4ac < 0. As it can be guessed, there is no solution: in , the term
is strictly positive, forbidding any remarkable identity.
To summarize, by adopting the notation ∆ = b2 – 4ac (∆ is called the “discriminant” because its value allows to discriminate between the different possible results):
If ∆ > 0, the equation has two solutions, which are:
If ∆ = 0, a double root exists:
And if ∆ < 0, there are no real roots (we will not cover here imaginary solutions).
We have retrieved the three cases we highlighted in the first part of this post.
We have found Al-Khwarizmi’s solutions with a slightly faster method (because more general, see the Wikipedia article regarding this point). But we must also notice that we come some twelve centuries later!
References (for the historical aspects):
http://en.wikipedia.org/wiki/Quadratic_equation#History
http://www-history.mcs.st-and.ac.uk/HistTopics/Quadratic_etc_equations.html